La navigation VFR

---

Au départ, le but de cette page était simplement d'expliciter les formules qui figurent sur cette merveille technologique qu'est le "rapporteur de déroutement" (muni de sa ficelle !). Mais elle permet également de comprendre les apparentes contradictions qu'un lecteur attentif ne manquera pas de relever lors de la lecture de certains ouvrages, même "officiels" !

---

Qu'est-ce que la navigation ?

C'est l'art d'aller d'un point à un autre de manière optimum en fonction de différentes contraintes souvent contradictoires (temps, coût, météo, trajet, étapes, poids, etc ...).

La formule de base en navigation est :

L = Vp * T

dans laquelle :

• L est la distance parcourue (en mètres),
• Vp est la vitesse propre (en mètres par seconde),
• T est le temps (en secondes) mis pour parcourir la distance L à la vitesse Vp.

La vitesse propre d'un avion est la projection de sa vitesse vraie Vv sur le plan horizontal (sol). En général, on prend Vp = Vv car la vitesse ascentionnelle est en générale faible par rapport à la vitesse vraie (une vitesse ascentionnelle de 1000 ft / mn = 0,164 Nm / mn = 9,8 Nm / h est faible par rapport à une vitesse vraie de 100 Nm / h ou plus ...).

On en déduit la formule inverse : T = L / Vp c'est à dire que pour obtenir le temps de parcours, il suffit donc de diviser la distance à parcourir par la vitesse.

Remarque : Les formules ci-dessus restent valables tant que l'on reste dans un système d'unités cohérentes. Ainsi :

• En navigation "terrestre" , on utilise plutôt les unités suivantes : L en kilomètres (km), Vp en kilomètres par heure (km/h), T en heures (h).
• En navigation "maritime", on utilise plutôt les unités suivantes : L en miles nautiques (Nm)), Vp en miles nautiques par heure ou noeuds (knt), T en heures (h).
  

En navigation "aéronautique", on préfère parfois exprimer le temps de parcours en minutes, avec toujours L en miles nautiques (Nm)) et Vp en miles nautiques par heure ou noeuds (knt), On n'est plus alors dans un système cohérent d'unités et il faut introduire un facteur correctif de 60 ( 1 noeud = 1 Nm / h = 1 / 60 Nm/minute). Les formules ci-dessus deviennent :

L = (Vp / 60) * T et T = L / ( Vp / 60 )

dans lesquelles :

• L est la distance parcourue ( en Nm),
• Vp est la vitesse propre ( en Nm / h ou noeuds),
• T est le temps (en minutes) mis pour parcourir la distance L à la vitesse Vp.

Le facteur de base :

On appelle "facteur de base" Fb le terme 60 / Vp . C'est en fait l'inverse d'une vitesse. Ce n'est donc pas un nombre sans dimension comme on le voit parfois écrit dans certains "cours". Pour obtenir le temps de parcours, il suffit donc de multiplier la distance à parcourir par le facteur de base. On a donc :

Fb = 60 / Vp et T = L * Fb

dans laquelle :

• L est la distance parcourue en Nm,
• Vp est la vitesse propre en Nm / h (ou noeuds),
• Fb est le facteur de base (en minutes / Nm),
• T est le temps (en minutes) mis pour parcourir la distance L à une vitesse correspondant au facteur de base Fb (ou, ce qui revient au même, à la vitesse Vp).

Route et Cap :

• Route ; C'est le tracé au sol de la ligne droite entre deux points.
• Cap : C'est l'orientation de l'avion qui permet de suivre la route.

Par vent nul, route et cap sont confondus. S'il y a du vent de travers, route et cap forment un angle appelé "dérive". Le vent souffle toujours du cap vers la dérive. On a :

Route = Cap + dérive

Triangle des vitesses :

La vitesse sol Vs d'un avion (par définition mesurée sur la route) est la résultante de sa vitesse propre Vp (par définition mesurée sur le cap) et de la vitesse du vent Vw. Le "triangle des vitesses" en est la représentation vectorielle.

Calcul de la dérive d :

Soit a "l'angle au vent" c'est à dire l'angle formé par la route suivie et le sens du vent.

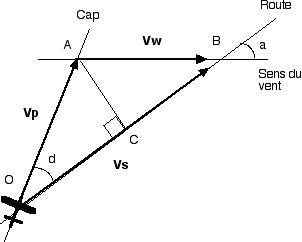Figure : 3

Dans les triangles rectangles OAC et ACB on peut écrire : AC = Vw * sin a et AC = Vp * sin d. D'où :  Vw * sin a = Vp * sin d et donc sin d = (Vw / Vp) * sin a , ce qui donne la formule exacte pour d  : d = Arcsin [ (Vw / Vp) * sin a ]

Quelques cas particuliers :

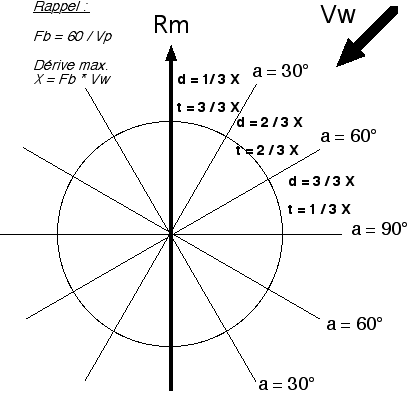
- 1/ Dérive max : Voir figure 4.

Figure : 4

L'expression générale de la dérive : d = Arcsin [ (Vw / Vp) * sin a  passe par un maximum, pour Vp et Vw donnés, pour a = 90° (sin 90° = 1). La dérive est donc maximale lorsque le vent est perpendiculaire à route suivie. Cette formule générale donne alors : sin d = (Vw / Vp) * sin(90°) = (Vw / Vp). Si on appelle X la dérive max, on a : sin X = Vw / Vp soit :  X  = Arcsin (Vw/Vp)

- 2/ Cas Vs = Vp : Voir figure 5.

Figure : 5

On voit que ce cas se produit lorsque le vent est perpendiculaire à la bissectrice de la dérive car le triangle OAB est alors isocèle. On a : Vs = Vp On appelle "vitesse de vent effectif" ou "vent effectif" Ve la quantité algébrique qu'il faut ajouter à la vitesse propre Vp pour obtenir la vitesse sol Vs ( Vs = Vp + Ve ).  On voit donc que, par définition, le vent effectif est nul lorsque le vent est perpendiculaire à la bissectrice de la dérive.

Vent effectif et vent traversier :

Nous avons défini Ve comme la quantité algébrique qu'il faut ajouter à la vitesse propre Vp pour obtenir la vitesse sol Vs. Si nous voulions pouvoir décomposer le vent en deux composantes : l'une Ve (vent effectif) parallèle à la route suivie, l'autre Vt (vent traversier), il nous faudrait alors définir le vent traversier comme la composante du vent Vw sur la perpendiculaire à la bissectrice de la dérive (voir figure 6 ). On a : Vs = ( Vp * cos d ) + (Vw * cos a), d'où :

Ve = Vs -Vp = (Vw * cos a ) - Vp ( 1 - cos d )

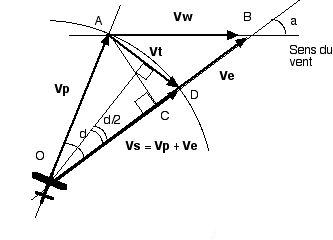Figure 6 (représentation exacte)	Figure 7 (représentation "simplifiée")

Simplification : Sachant que l'angle de dérive est en général faible, on prend cos d ~ 1 et l'on a alors : 

Vs ~ Vp + (Vw * cos a) avec : Ve ~ Vw * cos a

Ve ~ Vw * cos a et Vt ~ Vw * sin a 

Vent effectif et dérive max. :

Figure 8.

Nous avons vu que la dérive est maximale lorsque le vent est perpendiculaire à la route. Dans ce cas, la représentation de la figure 6 devient celle donnée figure 8 sur laquelle nous avons représenté le trajet aller et le trajet retour. On voit que dans ce cas (dérive maximale), on a un vent effectif contraire (négatif) aussi bien à l'aller qu'au retour. On a : Ve = Vw * tg (d/2) Cette quantité est souvent négligée (cas de la figure 7), sauf si Vp est faible et Vw fort.

Calcul mental de la dérive :

En vol, l'on n'a pas toujours le temps d'effectuer des calculs "compliqués". On a donc imaginé des formules "simplifiées" qui permettent d'obtenir un résultat numérique en un minimun de calculs.

Dérive maximum X

Dérive d.

On a vu (figure 4) que : X = Arcsin (Vw / Vp). - 1ère simplification : Dans la pratique, pour des angles faibles, disons inférieurs à 30°, on a Arcsin X ~ X, X étant exprimé en radian.  - 2ème simplification : 1 rd = 360° / 2 pi = 57,3 °. On prendra 1 rd ~ 60 degrés (soit pi = 3 au lieu de 3,14). D'où :  X (en rd) ~ Vw / Vp     ou encore : X (en °) ~ (Vw / Vp) * 60 Comme la quantité 60 / Vp est numériquement égale au facteur de base, on écrit un peu abusivement (en confondant les degrés d'angle avec les minutes de temps !)  X (en degrés) ~ Vw * Fb

On a vu (Figure 3) que la dérive est donnée par la formule : d = Arcsin [ (Vw / Vp) * sin a ] Avec les mêmes simplifications que pour la dérive max (voir ci-contre), on a :  d (en degrés) ~ 60* (Vw / Vp) * sin a soit : d (en degrés) ~ X * sin a Comme la quantité 60 / Vp est numériquement égale au facteur de base, on écrit un peu abusivement (en confondant les degrés d'angle avec les minutes de temps !) d (en degrés) ~ Vt * Fb

Temps "sans vent" et "avec vent" :

Formules dans lesquelles :

• L est la distance parcourue en Nm,
• Vp est la vitesse propre en Nm / h (ou noeuds),
• Vs est la vitesse sol en Nm / h (ou noeuds),
• Fb est le facteur de base (en minutes / Nm) correspondant à la vitesse Vp,
• T est le temps (en minutes) mis pour parcourir la distance L ).

On a donc : Tav = Tsv + ((Tav * Ve) / Vp).

Le temps avec vent (en minutes) est donc égal au temps sans vent (en minutes) plus ou moins (suivant le sens du vent) le terme de correction, lui aussi exprimé en minutes: Tav * Ve / Vp.

Il y a plusieurs manières d'utiliser cette formule :

- 1ère méthode : On pose y (en %) = Ve / Vp * 100 . La formule devient : Tav = Tsv + (Tav * y %). Pour un premier cacul on prendra, pour Tav du second membre, Tav = Tsv. C'est généralement suffisant et c'est pourquoi on rencontre parfois la formule : Tav  ~ Tsv + (Tsv * y %). Sinon, on refera un second calcul en prenant pour Tav la valeur que l'on vient de trouver (calcul par itération).

- 2ème méthode : On pose : t = Fb * Ve et on exprime le terme correctif Tav * Ve / Vp en secondes qui deviend donc : 60 * Tav * Ve / Vp.

On a donc : Tav = Tsv + (t * Tav), t étant exprimé en secondes par minute de vol.

Comme Ve = Vw * cos a, on remarque que t = Fb * Vw * cos a = X * cos a = X * sin (90° - a).

Comme précédemment, pour un premier cacul on prendra, pour Tav du second membre, Tav = Tsv. C'est généralement suffisant et c'est pourquoi on rencontre parfois la formule : Tav  ~ Tsv + (t * Tsv). Sinon, on refera un second calcul en prenant pour Tav la valeur que l'on vient de trouver (calcul par itération).

- 3ème méthode : On pose t' = (60 * t) / (60 + t) et l'on peut montrer alors que la formule devient alors : Tav = Tsv + (t' * Tsv). Cette formule sera notamment utilisée pour les calculs par ordinateur.

Et en pratique on fait quoi ?

Bien évidemment, il n'est pas question de faire en vol des calculs compliqués et compte-tenu en particulier des imprécisions sur la direction et la vitesse du vent, cela n'aurait aucun intérêt. Des valeurs approchées sont largement suffisantes. Plusieurs méthodes existent, en voici deux, parmi les plus simples et les plus rapides :

- 1ère méthode : Utilisée par exemple pour préparer un plan de vol, pour déterminer rapidemment l'effet du vent sur les différentes branches.

On calcule le facteur de base Fb = 60 / Vp et la dérive max X (en °)  ~ Vw * Fb. On trace alors le tableau suivant :

Angle au vent a (en °)	0-10	20	30	40	50	60	70	80-90
Sin (a)	0	0,3	0,5	0,6	0,7	0,8	0,9	1
Dérive d (en °)  ~ X * sin(a)	0	0,3*X	0,5*X	0,6*X	0,7*X	0,8*X	0,9*X	X
t (en secondes par minute de vol) = X * sin(90° - a)	X	0,9*X	0,8*X	0,7*X	0,6*X	0,5*X	0,3*X	0

Remarque : la dernière ligne est la recopie "à l'envers" de la ligne précédente (propriété de cos(a) = sin(90°-a)).

Exemple :

Hypothèse : Vp = 90 kt. Route magnétique suivie : Rm = 360° Vent du 40° pour 20 kt. L'angle au vent est donc de 40°

Résultats : Fb = 60 / 90 = 0,66 arondi à 0,7 X = 20 * 0,7 = 14° et donc : dérive d = 0,6 * X = 8° t = 0,7* X = 10 secondes de plus par minute de vol,  soit 16 % (10 / 60) de temps de vol en plus

- 2ème méthode : Encore plus simple, à utiliser en vol. Elle est cohérente avec la précision d'une navigation à vue sur avion de tourisme.  On considère seulement  3 secteurs : un premier secteur d'angle au vent compris entre 0 et 30°, un deuxième secteur d'angle au vent compris entre 30 et 60° et un troisième secteur d'angle au vent compris entre 60 et 90°.

Exemple : Vp = 90 kt. Route magnétique suivie : Rm = 360° Vent du 40° pour 20 kt. L'angle au vent est donc de 40° ; on est dans le second secteur. On a : Fb = 60 / 90 = 0,66 arondi à 0,7 X = 20 * 0,7 = 14° et donc : dérive d = 2/3 X = 9° t = 2/3 X = 9 secondes de plus par minute de vol soit 15 % (9 / 60) de temps de vol en plus.

 

Pente d'approche :

On peut définir une pente soit par son angle par rapport au sol , soit par un pourcentage noté ici x. Par analogie et cohérence vis-à-vis de la définition mathématique de la pente d'une droite (pente = dy / dx), on convient qu'une pente de 5 % signifie que pour une distance horizontale parcourue de 100 mètres la variation d'altitude est de 5 mètres (figure 6). On a ainsi : x (en %) = 100 * (Vz / Vs), Vs et Vz étant exprimés dans la même unité. Si on mesure maintenant Vs en noeuds et Vz en ft / minute, on a (car 1000 ft / mn = 0,164 Nm / mn = 9,8 Nm / h ~ 10 Nm / h) :

Vz (en ft/mn) ~ Vs (en knt) * x (en %)

Dans le triangle rectangle OAB, on a : tg i = OA / OB = Vz / Vs, Vs et Vz étant exprimés dans la même unité. Si Vs est en noeuds et Vz en ft / minute, on a (car 100 ft / mn ~ 1 Nm / h) : tg i ~ (Vz /100 ) / Vs.En faisant de plus les mêmes simplifications que pour le calcul de la dérive max (voir plus haut), on a : i (en degrés) ~ 60 * (Vz /100 ) / Vs = (6 /10) * Vz / Vs soit : i (en degrés) ~ 6 / 10 * x (en %) Une pente de 5 % correspond ainsi à un angle i de 3 degrés.

Temps de descente :

L'altitude est mesurée en pieds (ft), la vitesse de descente en ft / minute, le temps mis pour descendre d'une hauteur h est donc :

Temps (en minutes) = Hauteur (en ft) / Vz (en ft / mn)

Le rapporteur de déroutement

La règle vectorielle

Il existe une "règle vectorielle", de fabrication française et conçue par un pilote-instructeur, qui illustre parfaitement l'utilisation du triangle des vitesses. Cette règle permet de calculer en quelques secondes la dérive et le cap à suivre en fonction de la vitesse de l'avion et de celle du vent, pour une route donnée. Sur l'exemple ci-contre (cliquer sur l'image pour l'agrandir), on voit que pour une route au 010° (lue sur la graduation extérieure du rapporteur), un vent de 18 kt au 228° (lue sur la graduation intérieure du rapporteur) et une IAS de 123 km/h, on a une dérive de 10° et un cap plein nord à suivre. La vitesse sol est alors de 148 km/h. C'est immédiat ! Il existe un modèle "faibles vitesses" avec IAS en km/h et un modèle "vitesses fortes" avec IAS en kt. Télécharger le mode d'emploi (en français). Download the user manual (in English). Pour plus d'informations, voir le site de son concepteur ici. Bernard DELPOUVE ULMVIENNE Reventin-Vaugris (38)

Quelques rappels sur les unités :

- Foot (ft) : Le "pied", en anglais foot (pluriel feet) est une unité de longueur utilisée dans différents systèmes d'unité et sa valeur dépend du système d'unité choisi. Le plus utilisé est aujourd'hui est le "international foot". Il y a 3 feet (pieds) dans un yard et 12 inches (pouces) dans un foot (pied).
En 1958, les USA et certains états du Commonwealth ont défini le yard international comme étant égal à : 0.9144 mètres. En conséquence, un pied (international foot) vaut : 0.3048 mètres. Le symbole international du pied est : ft.

- Mile nautique (NM) : Depuis 1929, le mile nautique international (international nautical mile) est défini comme étant exactement égal à 1852 mètres. Historiquement, le mile nautique était défini comme la longueur d'un arc de grand cercle (équateur ou méridiens) de la terre engendré par un angle au centre de 1 minute d'angle. Seulement voilà, la terre n'est pas une sphère parfaite ... La valeur 1852 mètres adoptée en 1929 est en fait très proche (à 0,01% près) de la valeur moyenne d'une minute de latitude (1852,235 mètres). Il n'y a pas de symbole international défini pour le mile nautique. Parmi les symboles les plus utilisés, NM est l'un de ceux qui prête le moins à confusion (à la différence de nm : nanomètre - ou Nm : Newton-mètre par exemple).

Les relations entre le mile nautique et le pied (foot) sont très ambigues ... Il résulte des références ci-dessus prises par rapport au système métrique qu'il y a 6076,115... feet dans un mile nautique.  Mais, suivant les époques ou les utilisateurs, cela va de 6000 à 6080 voire 6080,2 feet pour un mile nautique.

- Noeud (kn) :  Un noeud est une unité de vitesse définie comme 1 NM / heure. Il n'y a pas de symbole international défini pour le noeud (knot en anglais). On utilise généralement kn, kt ou knt.

Plus d'infos sur les unités ? Voir le site du Bureau international des Poids et Mesures.

---

Retour page simulation

Page suivante

Retour page d'accueil