Wing loading and slow-fly

Introduction:

When you simply scale down to 1/r only the physical dimensions of a model, then:

• distances (and therefore speed v, distance per time unit) are reduced by a factor r,
• surfaces, by a factor r to the square,
• volumes, by a factor r to the cube.

Nota:
1/ Mass (m) are also reduced by a factor r to the cube if we suppose that the structures and materials used are fairly similar.
2/ Time is supposed to be constant and independent from the scale (see below).

In these conditions, it can be shown (see Ib Therkelsen's page or download the article in MSWord format) that:

• The wing loading (z) is reduced by a factor r and varies as the cubic root of the masses (z2=z1 x cubic root (m2/m1),
• The speed is reduced by a factor square root of r (sqr(r)), if we suppose that the lift coefficient CL is identical between the two models.

And now, we have got a problem...

As a matter of fact, to keep the scale speed of a cruise flight, speed should be reduced by a factor r (and not sqr(r) ) as the plane should for instance cover its own length during the same time. To achieve such a result, we therefore have to modify at least one of the hypothesis we made above (masses reduced by r to the cube, lift coefficient and time independent from the scale).

If we play only on mass ratio, which seems to be the easiest way, and therefore keeping the time and the lift coefficient constant, we can demonstrate that the model mass has to be reduced by a factor r to the fourth power (and not to the cube) to have this model fly at a speed to the scale 1/r. Then, we have the following relations:

Considering the lift coefficient CL as constant between a full scale plane and a scale 1/r model could be considered as questionable; however, it can be considered as valid when making comparison between scale models. To illustrate this, you will find hereafter wing loading values (z) versus masses (m) of different slow-fliers models (between 9 and 300 grammes).

According to these results, it seems that between models with similar flight performances ( here, slow-fly category ) we have the relation z2/z1= sqr(m2/m1) (continuous line curve).

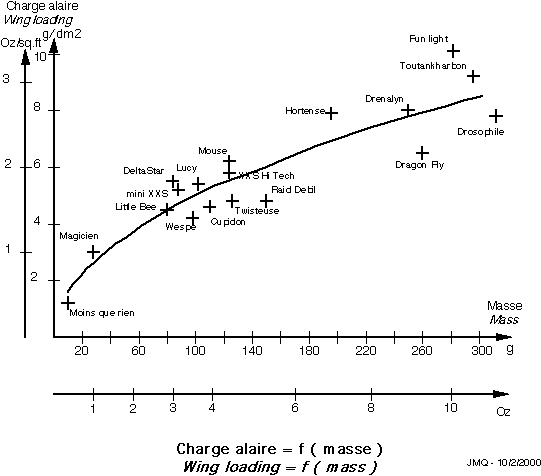
Any model deviating notably from the above curve (upwards) should be more and more difficult, even impossible to control.

Remark:

A different approach to this problem would be to consider the time as variable with the scale. At first glance, this could seem to be a little bit surprising. However, it is exactly what is used by special effects in movies ( shooting of a model train derailment or an model explosion with an high speed camera and playing back the film at normal speed). We can demonstrate ( "Understanding scale speed" by Bob Boucher ) that the scale time should run faster than real time by an amount equal to the square root of the scale factor r. In these conditions, the relation v2=v1/r (i.e. L2/t2=(L1/t1)/r with now t2/t1=sqr(r) ) becomes v2 = v1/sqr(r), which is the relation mentioned at the beginning when considering only the scaling of physical dimensions...

Now, I am sure you are ready for reading the theories of a certain Albert Einstein on time-space and relativity (restricted for a start). Have a good flight all the same !