Charge alaire et Slow-fly

Introduction:

Une simple mise à l'échelle 1/r des dimensions physiques d'un modèle conduit à ce que:

• les longueurs (et donc les vitesses v, longueur par unité de temps) soient réduites d'un facteur r,
• les surfaces, d'un facteur r au carré,
• les volumes, d'un facteur r au cube.

Nota:
1/ les masses (m) sont également réduites dans le rapport r au cube (en supposant que les techniques de construction et les matériaux utilisés soient les mêmes).
2/ le temps est ici supposé incompressible et indépendant de l'échelle (voir plus loin).

Dans ces conditions, on peut montrer (voir la page de Ib Therkelsen ou télécharger l'article au format MSWord) que:

• La charge alaire (z) est réduite d'un facteur r et varie comme la racine cubique des masses (z2=z1 x racine cubique (m2/m1),
• La vitesse est réduite d'un facteur racine carrée de r (sqr(r)), ceci en supposant un coefficient de portance CL identique entre les deux modèles.

Et c'est là le hic...

En effet, pour conserver une allure "à l'échelle" en vol de croisière, la vitesse devrait être réduite dans le rapport r ( et non sqr(r) ) car l'avion doit parcourir par exemple sa propre longueur (à l'échelle 1/r) pendant le même temps. Pour arriver à un tel résultat, il faut donc modifier l'une au moins des trois hypothèses faites ci-dessus (masses réduites dans le rapport r au cube, coefficient de portance et temps indépendants de l'échelle).

En jouant sur le rapport des masses, ce qui semble à priori le plus facile, et donc en conservant constant le temps et le coefficient de portance, on montre que la masse d'un modèle doit être réduite dans le rapport r à la puissance 4 (et non au cube) pour que le modèle vole à une vitesse "à l'échelle" 1/r. On a donc alors les relations suivantes:

S'il peut paraître discutable de considérer que le coefficient de portance CL est le même pour un avion grandeur et son modèle à l'échelle 1/r, on peut admettre que cela est vrai quand il s'agit de comparer des modèles réduits entre eux. A titre d'exemple, on trouvera ci-dessous les valeurs de charge alaire z relevées sur différents modèles de "Slow-fliers" en fonction de leur masse m (entre 9 et 300 grammes).

Il semble bien, d'après ces résultats que des modèles ayant un comportement en vol similaire (ici catégorie slow-fly) suivent bien une loi du type z2/z1= sqr(m2/m1) (courbe en trait plein).

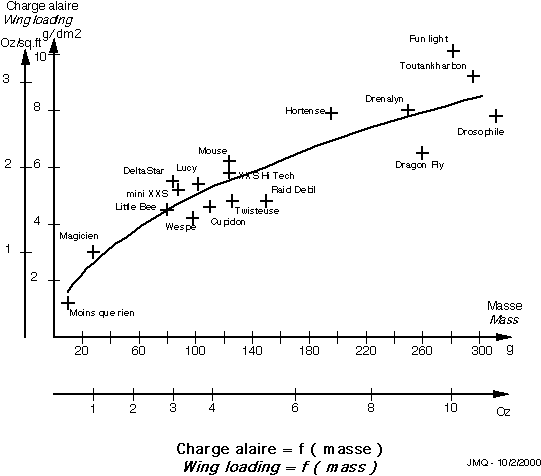
Tout modèle s'écartant notablement de cette courbe (vers le haut) aura un comportement de plus en plus difficile, voire impossible à contrôler.

Remarque:

Une autre approche consisterait à considérer le temps comme variable avec l'échelle. Ceci peut paraître surprenant à première vue mais c'est pourtant ce qui est utilisé dans les effets spéciaux au cinéma par exemple ( tournage en accéléré d'une explosion, d'un déraillement, etc..., d'une maquette et projection à vitesse normale, avec un réalisme saisissant ). On peut montrer (voir "Understanding scale speed" by Bob Boucher) que le temps "à l'échelle" doit s'écouler plus rapidement que le temps réel dans le rapport racine de r. Dans ces conditions, la relation v2=v1/r (qui peut s'écrire L2/t2=(L1/t1)/r avec t2/t1=sqr(r) ) devient v2 = v1/sqr(r), relation à laquelle nous avions abouti en considérant une simple mise à l'échelle des dimensions physiques...

Maintenant je vous sens mûr pour lire les théories d'un certain Albert Einstein sur l'espace-temps et la relativité (restreinte, pour commencer). Bons vols quand même!